ANGULOS

RETO MATEMÁTICO

ANGULOS

En geometría, el ángulo puede ser definido como la parte del plano determinada por dos semirrectas llamadas lados que tienen el mismo punto de origen llamado vértice del ángulo.¹​

La medida de un ángulo es considerada como la longitud del arco de circunferencia centrada en el vértice y delimitada por sus lados. Su medida es un múltiplo de la razón entre la longitud del arco y el radio. Su unidad natural es el radián, pero también se puede utilizar el grado sexagesimal o el grado centesimal.

Pueden estar definidos sobre superficies planas (trigonometría plana) o curvas (trigonometría esférica). Se denomina ángulo diedro al espacio comprendido entre dos semiplanos cuyo origen común es una recta. Un ángulo sólido es el que abarca un objeto visto desde un punto dado, midiendo su tamaño aparente.

Clasificación de ángulos según su medida

Ángulo agudo

 Mide menos de .

Ángulo recto

 Mide .

Ángulo obtuso

 Mide más de .

Ángulo llano

 Mide .

Ángulo convexo

 Mide menos que un ángulo llano.

Ángulo cóncavo

 Mide más que un ángulo llano.

Ángulo nulo

 Mide . Las semirrectas que forman los ángulos coinciden.

Ángulo completo

 Mide .

Ángulo negativo

 Mide menos de .

Los ángulos negativos giran en el sentido horario, es decir, en el sentido en que se mueven las agujas de un reloj.

Un ángulo negativo lo podemos transformar en un ángulo positivo sumándole .

Ángulo mayor de 360°

Mide más de una vuelta.

Un ángulo de , si lo representamos coincide con un ángulo de . Un ángulo de , si lo representamos coincide con un ángulo de . Si queremos pasar un ángulo a la primera vuelta, dividimos el ángulo entre : El cociente es el número de vueltas que da.El resto es ángulo resultante que corresponde a la primera vuelta.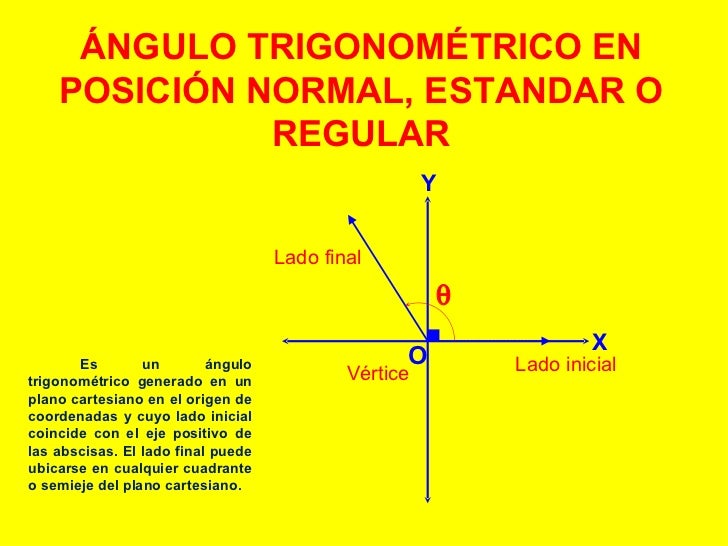

 

ACTIVIDAD

Dibujar y clasificar los siguientes ángulos en posición normal

1. 50° 

2. -30°

3. 170°

4. -435°

5. 780°

6. -450º

7. 800º

8. -560º

9. -230º

10- 1000º