CIRCUNFERENCIA UNITARIA
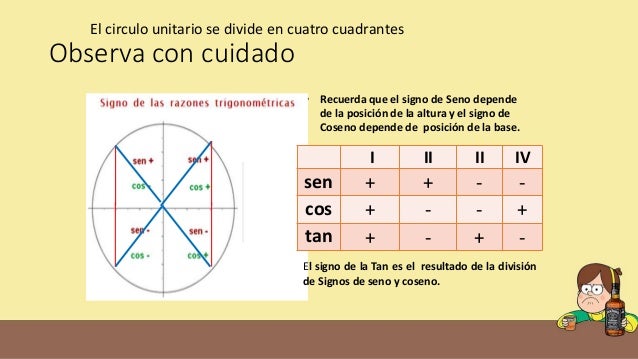
La circunferencia goniométrica, trigonométrica, unitaria, es una circunferencia de radio uno, normalmente con su centro en el origen (0, 0) de un sistema de coordenadas, de un plano euclídeo o complejo. Dicha circunferencia se utiliza con el fin de poder estudiar fácilmente las razones trigonométricas y funciones trigonométricas, mediante la representación de triángulos rectángulos auxiliares.
Si (x, y) es un punto de la circunferencia unidad del primer cuadrante, entonces x e y son las longitudes de los catetos de un triángulo rectángulo cuya es hipotenusa tiene longitud 1. Aplicando el teorema de Pitágoras, a y b
-
-
-
-
- radio = hipotenusa. ____TEOREMA DE PITAGORAS PARA LA CIRCUNFERENCIA UNITARIA

Funciones trigonométricas en la circunferencia unitaria[editar]
Si (x, y) es un punto de la circunferencia unidad, y el radio que tiene el origen en (0, 0), forma un ángulo con el eje X, las principales funciones trigonométricas se pueden representar como razón de segmentos asociados a triángulos rectángulos auxiliares, de la siguiente manera:y dado que la hipotenusa es igual al radio, que tiene valor = 1, se deduce:El coseno es la razón entre el cateto adyacente (b) y la hipotenusa (c)y como la hipotenusa tiene valor = 1, se deduce:La tangente es la razón entre el cateto opuesto y el adyacentePor semejanza de triángulos:como se deduce que:Funciones trigonométricas recíprocas.[editar]
La cosecante, la secante y la cotangente, son las razones trigonométricas recíprocas del seno, coseno y tangente:Los valores de la cotangente, la secante y la cosecante se obtienen, análogamente, mediante semejanza de triángulos.
- EJEMPLO


- ACTIVIDAD
- Determinar las razones trigonometricas para los puntos dados en la siguiente circunferencia unitaria


-
-
-

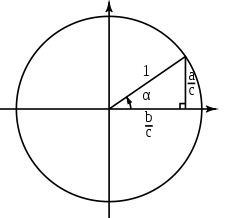

 con el eje X, las principales funciones trigonométricas se pueden representar como
con el eje X, las principales funciones trigonométricas se pueden representar como 













No hay comentarios.:
Publicar un comentario